[ECCV22] Learning Algebraic Representation for Systematic Generalization in Abstract Reasoning
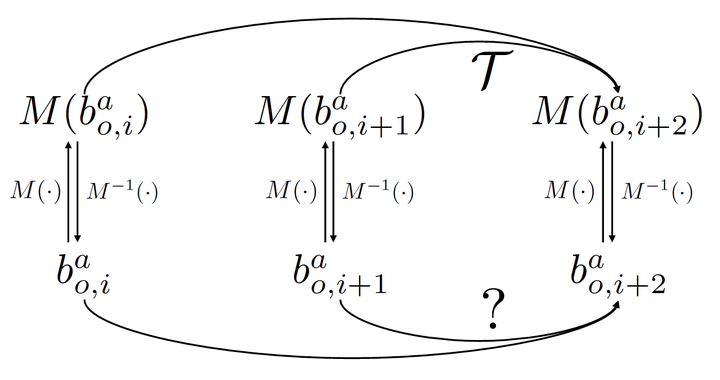
Abstract
Is intelligence realized by connectionist or classicist? While connectionist approaches have achieved superhuman performance, there has been growing evidence that such task-specific superiority is particularly fragile in systematic generalization. This observation lies in the central debate between connectionist and classicist, wherein the latter continually advocates an algebraic treatment in cognitive architectures. In this work, we follow the classicist’s call and propose a hybrid approach to improve systematic generalization in reasoning. Specifically, we showcase a prototype with algebraic representation for the abstract spatial-temporal reasoning task of Raven’s Progressive Matrices (RPM) and present the ALgebra-Aware Neuro-Semi-Symbolic (ALANS) learner. The ALANS learner is motivated by abstract algebra and the representation theory. It consists of a neural visual perception frontend and an algebraic abstract reasoning backend: the frontend summarizes the visual information from object-based representation, while the backend transforms it into an algebraic structure and induces the hidden operator on the fly. The induced operator is later executed to predict the answer’s representation, and the choice most similar to the prediction is selected as the solution. Extensive experiments show that by incorporating an algebraic treatment, the ALANS learner outperforms various pure connectionist models in domains requiring systematic generalization. We further show that the generative nature of the learned algebraic representation; it can be decoded by isomorphism to generate an answer.